2級ﾌｧｲﾅﾝｼｬﾙ・ﾌﾟﾗﾝﾆﾝｸﾞ技能士（FP2級） 過去問
2025年5月（CBT）
問91 (実技 問31)

この問題は6つの係数について問われています。

6つの係数は以下の通りです。

■終価係数：今ある金額が、将来いくらになるかを計算する係数

■現価係数：将来の目標を達成するため、今いくら必要かを計算する係数

■年金終価係数：毎年同じ金額を積み立てた場合、将来いくらになるかを計算する係数

■減債基金係数：将来の目標額を達成するため、毎年いくら積み立てるべきかを計算する係数

■年金現価係数：毎年同じ金額ずつ返済する場合、いくら借りることができるか計算する係数

■資本回収係数：借入金を毎年いくら返済するかを計算する係数

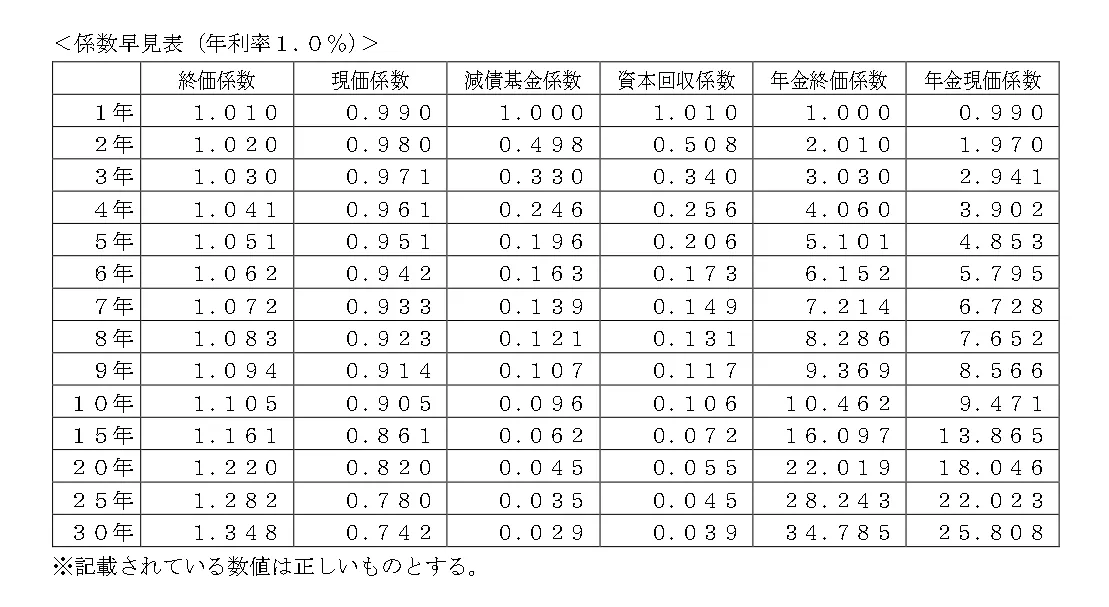
設問の場合は「9年間、年利1.0％で複利運用する場合、現在いくらの資金があればよいか」を問われていますので現価係数を使用します。

計算式は以下の通りです。

400万円×0.914＝3,656,000

従って3,656,000円になります。

6つの係数を用いて計算する問題です。

終価係数：今ある金額を一定期間複利運用した場合の将来価格を求める際に用いる

現価係数：将来の目標額を達成するのに必要な現在価格を求める際に用いる

減債基金係数：将来の目標額を達成するために毎年必要な積立額を求める際に用いる

資本回収係数：一定金額を一定期間複利運用して毎年受け取る金額を求める際に用いる

年金終価係数：一定金額を毎年複利運用して積み立てた場合の将来価格を求める際に用いる

年金現価係数：一定金額を一定期間に受け取る場合に必要な現在価格を求める際に用いる